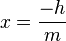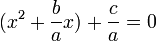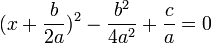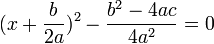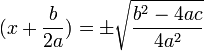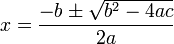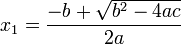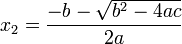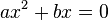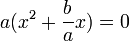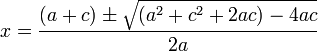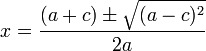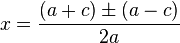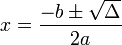حل معادلات درجهٔ دوم
همانند حل معادلات درجهٔ اول برای پیدا کردن نقاط تقاطع معادله با محور xها صورت کلی معادلات درجه دوم را نوشته و عرض آن ( y ) را برابر صفر قرار می دهیم، پس داریم :
با حل معادله ی فوق مقادیر x را بدست می آوریم، توجه کنید که a برابر با صفر نمیتواند باشد چون در این صورت معادله از نوع درجه اول میشود. پس با شرط a≠0 معادله را حل می کنیم :
اگر ضرب چند عبارت برابر با صفر باشد پس حداقل یکی از آنها صفر است، از آنجا که a بنا بر شرط اولیه نمیتواند صفر باشد پس عبارت داخل پرانتر صفر میباشد، پس داریم :
برای حل معادله آن را تبدیل به مربع کامل می کنیم :
حالا از طرفین معادله جذر می گیریم تا مقدار x را درآوریم :
در نتیجه معادله دارای 2 ریشهٔ زیر میباشد:
معمولاً عبارترا برابر با حرف دلتای بزرگ
نمایش میدهند، دلتا در ریاضیات نماد فاصله یا تغییرات است.طبق قضیهٔ تثلیث دلتا میتواند مقادیر زیر را اختیار کند :
1 -که در آن صورت فاصلهٔ بین دو ریشه مثبت است، پس معادله دو ریشهٔ مختلف دارد
2 -که در آن صورت فاصلهٔ بین دو ریشه صفر است، پس هر دو جواب معادله یکی هستند و معادله اصطلاحاً ریشهٔ مضاعف دارد
3 -که در آن صورت فاصلهٔ بین دو ریشه عددی منفی است و همانطور که می دانید فاصله عددی منفی نمیتواند باشد، از سوی دیگر از آنجا که
در زیر رادیکالی با فرجهٔ زوج است تنها میتواند مقادیر بزرگتر یا مساوی صفر را اختیار کند.
حالتهای خاص و نکات معادلات درجهٔ دومدر معادلهٔ کلی
، اگر :
1 - c=0 باشد : یک ریشه صفر و دیگری برابر بااست.
اثبات ( شرط : a≠0 و c=0 ) :
2 - جمع 3 ضریب ( a,b,c ) برابر صفر باشد : یک ریشه +1 و دیگریخواهد بود
اثبات ( شرط : a≠0 و a+b+c=0 ) :
طبق فرض : a+b+c = 0 پس : a+c = -b
بد نیست که در باره ای ریشه مضاعف بشتر بدانیم: از نظر جبری ریشه مضاعف ریشه ای است که زوج بار عبارت را صفر کند و ریشه ساده ریشه ای است که فرد بار یک عبارت را صفر کند ((البته در معادلاتی نظیر 2^(x-1) همین تعریف کافی است ولی در دو طرف ریشه ساده علامت تابع فرق می کند ولی در دو طرف ریشه مضاعف علامت تابع یکسان است از نظر هندسی اگر بر محور طول ها طوری مماس شود که دو طرف نقطه در یک طرف محور طول ها بیفتد ریشه مضاعف داریم این نکته را فراموش نکنید که اگر رشه معادلات درجه دو مضاعف باشد آن معادله مربع کامل است
3 - a-b+c = 0 : یک ریشه -1 و دیگریخواهد بود
اثبات ( شرط : a≠0 و a-b+c=0 ) :
همانند روش بالا اثبات خواهد شد
4 - اگر دلتای ریشههای یک معادله برابر صفر باشد معادله تنها دارای یک جواب ( ریشه مضاعف )خواهد بود.
اثبات ( شرط : a≠0 وهمچنین جالب است بدانید مجموع دو ریشه در معادلهٔ درجه دوم)
نکته : همانطور که می دانید در صورتی که معادله دارای یک ریشه باشد یعنی تنها یک نقطهٔ تماس با محور xها دارد، در این صورت آن نقطه
تنها میتواند نقطهٔ مینیمم یا ماکسیمم باشد، پس داریم :
با گرفتن مشتق داریم :
است . ضمن اینکه ضرب دو ریشهٔ معادلهٔ درجه دوم از رابطهٔ
به
دست می آید.

 میباشد که در آن
میباشد که در آن  عرض اصلی ،
عرض اصلی ، 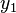 عرض اولیه ، m شیب نمودار و x متغیر طول نمودار میباشد، همچنین در اکثر منابع شکل اصلی معادلات درجهٔ اول به صورت
عرض اولیه ، m شیب نمودار و x متغیر طول نمودار میباشد، همچنین در اکثر منابع شکل اصلی معادلات درجهٔ اول به صورت 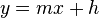 نمایش داده میشود که در آن h همان عرض اولیه است که به اختصار از کلمهٔ height استفاده میشود
نمایش داده میشود که در آن h همان عرض اولیه است که به اختصار از کلمهٔ height استفاده میشود